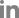ņä£ ļĪĀ
ļ®öĒāĆļČäņäØņØĆ ĒŖ╣ņĀĢ ņŻ╝ņĀ£ņŚÉ ļīĆĒĢ┤ ņ¦ĆĻĖłĻ╣īņ¦Ć ļ░£Ēæ£ļÉ£ ļ¬©ļōĀ ņŚ░ĻĄ¼ļōżņØä Ļ▓ĆĒåĀĒĢśĻ│Ā ņ▓┤Ļ│äņĀüņ£╝ļĪ£ Ļ▓░Ļ│╝ļź╝ ņłśņ¦æĒĢ£ Ēøä ņØ╝ņĀĢĒĢ£ ļ░®ņŗØņ£╝ļĪ£ ĒåĄĒĢ®ĒĢśņŚ¼ Ļ▓░ļĪĀņØä ņ¢╗ļŖö ĒåĄĻ│äņĀü ļ░®ļ▓Ģņ£╝ļĪ£, Ļ░£ļ│ä ņŚ░ĻĄ¼ņŚÉņä£ ĻĖ░ļīĆĒĢĀ ņłś ņŚåļŖö ļåÆņØĆ ņĀĢļ░ĆļÅäņØś Ļ▓░Ļ│╝ļź╝ ņĀ£Ļ│ĄĒĢ£ļŗżļŖö Ļ▓āņØ┤ ņĄ£ļīĆ ņןņĀÉņØ┤ļŗż[1,2]. ļö░ļØ╝ņä£ ņŚ░ĻĄ¼ Ļ▓░Ļ│╝ļōżņØ┤ ņä£ļĪ£ ņāüļ░śļÉ£ Ļ▓ĮņÜ░ļéś Ļ░£Ļ░£ņØś ņŚ░ĻĄ¼ Ļ▓░Ļ│╝ļōżņØ┤ Ļ▓ĮĒ¢źņä▒ņØĆ ņ׳ņ¦Ćļ¦ī ĒåĄĻ│äņĀü ņ£ĀņØśņä▒ņØĆ ņŚåļŖö Ļ▓ĮņÜ░ņŚÉ ļ®öĒāĆļČäņäØņØä ņŗ£Ē¢ēĒĢ┤ ļ│┤ļ®┤ ļ¬ģĒÖĢĒĢ£ Ļ▓░ļĪĀņØä ņ¢╗ņØä ņłś ņ׳ļŗż. ļśÉĒĢ£ ĒśäļīĆ ņØśĒĢÖņØś ĒĢĄņŗ¼ņØĖ ĻĘ╝Ļ▒░ņżæņŗ¼ ņØśĒĢÖņŚÉņä£ļÅä Ļ░Ćņן ļåÆņØĆ ņłśņżĆņØś ĻĘ╝Ļ▒░Ļ░Ć ļ¼┤ņ×æņ£ä ļīĆņĪ░ĻĄ░ ņŚ░ĻĄ¼ļōżņØä ļ¬©ņĢäņä£ ņŗ£Ē¢ēĒĢ£ ļ®öĒāĆļČäņäØņØĖ Ļ▓āņØä ļ│┤ļ®┤ ļ®öĒāĆļČäņäØņØś ņżæņÜöņä▒ņØä ņĀłĻ░ÉĒĢśĻ▓ī ļÉ£ļŗż[3]. ņØ┤ļ╣äņØĖĒøäĻ│╝ ņśüņŚŁņØś ņŻ╝ņĀ£ņŚÉ ļīĆĒĢ┤ņä£ļÅä ļŗżņłśņØś ļ®öĒāĆļČäņäØņØ┤ ņŗ£Ē¢ēļÉśņŚłņ£╝ļ®░, ņØ┤ ņżæ ņāüļŗ╣ņłśļŖö ĻĄŁļé┤ ņŚ░ĻĄ¼ņ×ÉļōżņØś ņŚģņĀüņØ┤ļŗż.
ļ®öĒāĆļČäņäØņØĆ ņØ╝ļ░śņĀüņØĖ ĒåĄĻ│ä ļČäņäØĻ│╝ļŖö ļŗżļźĖ ļÅģĒŖ╣ĒĢ£ ļ░®ņŗØņ£╝ļĪ£ ņ¦äĒ¢ēļÉśĻĖ░ ļĢīļ¼ĖņŚÉ ņ¦üņĀæ ņŗ£Ē¢ēĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ļ®öĒāĆļČäņäØņŚÉ ļīĆĒĢ£ ļ│äļÅäņØś ĒĢÖņŖĄĻ│╝ ĒŖ╣ļ│äĒĢ£ ĒåĄĻ│ä ĒöäļĪ£ĻĘĖļשņØ┤ ĒĢäņÜöĒĢśļŗż. ļśÉĒĢ£ ņŻ╝ņĀ£ ņäĀņĀĢņŚÉņä£ ļ¼ĖĒŚī Ļ│Āņ░░, ņ×ÉļŻī ņłśņ¦æ ļ░Å ņĀĢļ”¼ņŚÉ ņØ┤ļź┤ĻĖ░Ļ╣īņ¦Ć ņāüļŗ╣ĒĢ£ ņŗ£Ļ░äļÅä Ļ▒Ėļ”░ļŗż. ļ░śļ®┤ ļ®öĒāĆļČäņäØņØĆ ņןņĀÉļÅä ļ¦ÄņØĆļŹ░, ņØĖņÜ®ņØ┤ ņל ļÉśĻĖ░ ļĢīļ¼ĖņŚÉ ļåÆņØĆ ņłśņżĆņØś ņ×Īņ¦ĆņŚÉ ņ▒äĒāØļÉśļŖö Ļ▓ĮņÜ░ļÅä ļ¦ÄĻ│Ā, ņŻ╝ņĀ£ļÅä ļ¼┤ĻČüļ¼┤ņ¦äĒĢśļ®░, Ēü░ ļ╣äņÜ®ņØ┤ ļōżņ¦Ć ņĢŖļŖöļŗż.
ļ│Ė ņóģņäżņŚÉņä£ļŖö ļ®öĒāĆļČäņäØņØś Ļ░£ļģÉņŚÉ ļīĆĒĢ┤ Ļ░äļץĒ׳ ņåīĻ░£ĒĢśĻ│Ā ņĀĆņ×ÉņØś Ļ▓ĮĒŚśņØä ņĪ░ĻĖł ņ▓©Ļ░ĆĒĢśņŚ¼ ņāłļĪ£ņØ┤ ļ®öĒāĆļČäņäØņØä ņŗ£Ē¢ēĒĢśĻ│Āņ×É ĒĢśļŖö ņŚ░ĻĄ¼ņ×ÉļōżņŚÉĻ▓ī ļÅäņøĆņØä ņŻ╝Ļ│Āņ×É ĒĢśņśĆļŗż.
ļ®öĒāĆļČäņäØņØś 5ļŗ©Ļ│ä
ņØ╝ļ░śņĀüņ£╝ļĪ£ ļ®öĒāĆļČäņäØņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØĆ 5ļŗ©Ļ│äļĪ£ ņ¦äĒ¢ēļÉ£ļŗż[1].
ŌĆóņŚ░ĻĄ¼ņŻ╝ņĀ£ ņäĀņĀĢ ļ░Å ņŚ░ĻĄ¼ ņ¦łļ¼Ė ņĀ£ĻĖ░
ŌĆóĻ┤ĆļĀ© ļ¼ĖĒŚīņØś ņ▓┤Ļ│äņĀü Ļ▓Ćņāē
ŌĆóņŚ░ĻĄ¼ņØś ņ¦ł Ļ▓Ćņ”Ø ļ░Å ļŹ░ņØ┤Ēä░ ņĮöļö®
ŌĆóļŹ░ņØ┤Ēä░ ļČäņäØ
ŌĆóĻ▓░Ļ│╝ ļ│┤Ļ│Ā
Ļ░ü ļŗ©Ļ│äņŚÉ ļīĆĒĢ┤ ņóĆ ļŹö ņ×ÉņäĖĒ׳ ņé┤ĒÄ┤ļ│┤ĻĖ░ļĪ£ ĒĢśņ×É.
ņŚ░ĻĄ¼ņŻ╝ņĀ£ ņäĀņĀĢ ļ░Å ņŚ░ĻĄ¼ņ¦łļ¼Ė ņĀ£ĻĖ░
ļ®öĒāĆļČäņäØņØś ņŚ░ĻĄ¼ņŻ╝ņĀ£ļĪ£ļŖö ņ×äņāüņĀüņ£╝ļĪ£ ņØśļ»ĖĻ░Ć Ēü¼ļ®┤ņä£ ņāüļ░śļÉ£ Ļ▓░Ļ│╝Ļ░Ć ļ░£Ēæ£ļÉśņ¢┤ ņĢäņ¦ü ļ¬ģĒÖĢĒĢ£ Ļ▓░ļĪĀņØ┤ ņØ┤ļź┤ņ¦Ć ļ¬╗ĒĢ£ ņĢĮļ¼╝ņØ┤ļéś ņ╣śļŻīļ▓Ģ ļō▒ņØ┤ ņØ┤ņāüņĀüņØ┤ņ¦Ćļ¦ī, ĒŖ╣ļ│äĒĢ£ ĻĖ░ņżĆņØ┤ ņ׳ļŖö Ļ▓āņØĆ ņĢäļŗłļŗż. ņŚ░ĻĄ¼ņŻ╝ņĀ£Ļ░Ć ņäĀņĀĢļÉśļ®┤ ņØ╝ļŗ© ļīĆļץņĀüņØĖ Ļ▓ĆņāēņØä ĒĢ┤ ļ│┤ļŖö Ļ▓āņØ┤ ņóŗļŗż. Ļ░Ćņן ļ©╝ņĀĆ ĻĘĖ ņŚ░ĻĄ¼ņŻ╝ņĀ£ļĪ£ ņØ┤ļ»Ė ļ░£Ēæ£ļÉ£ ļ®öĒāĆļČäņäØņØ┤ ņ׳ļŖöņ¦Ć ņ░ŠņĢäļ│┤ņĢäņĢ╝ ĒĢ£ļŗż. ņØ┤ļ»Ė Ļ░ÖņØĆ ņŚ░ĻĄ¼ņŻ╝ņĀ£ņØś ļ®öĒāĆļČäņäØņØ┤ ņ׳ļŗżļ®┤ ĻĘĖ ņŚ░ĻĄ¼ņŻ╝ņĀ£ļź╝ ĒżĻĖ░ĒĢśļŹśņ¦Ć ļ░öĻŠĖņ¢┤ņĢ╝ ĒĢ£ļŗż. ļŗżļ¦ī, Ļ░ÖņØĆ ņŚ░ĻĄ¼ņŻ╝ņĀ£ņØś ļ®öĒāĆļČäņäØņØ┤ ņśżļלņĀäņŚÉ ļ░£Ēæ£ļÉ£ Ļ▓āņØ┤ļØ╝ļ®┤, ĻĘĖ ņé¼ņØ┤ņŚÉ ņāłļĪ£ ņČ£Ļ░äļÉ£ ļģ╝ļ¼ĖļōżņØä ņČöĻ░ĆĒĢ┤ņä£ ļŗżņŗ£ ļ®öĒāĆļČäņäØņØä ĒĢ┤ļ│╝ ņłś ņ׳ļŗż. ĻĘĖ ļŗżņØīņ£╝ļĪ£ļŖö ļ®öĒāĆļČäņäØņØä ņŗ£Ē¢ēĒĢĀ ļģ╝ļ¼ĖņØ┤ ņČ®ļČäĒ׳ ņ׳ļŖöņ¦Ć ĒÖĢņØĖĒĢ┤ ļ│┤ņĢäņĢ╝ ĒĢ£ļŗż. ņØ┤ļĪĀņĀüņ£╝ļĪ£ļŖö 2Ļ░£ņØś ļģ╝ļ¼Ėļ¦ī ņ׳ņ¢┤ļÅä ļ®öĒāĆļČäņäØņØ┤ Ļ░ĆļŖźĒĢśņ¦Ćļ¦ī, ņĢäļ¼┤ļלļÅä ļČäņäØĒĢĀ ņ×ÉļŻīĻ░Ć ļ¦ÄņĢäņĢ╝ Ļ▓░Ļ│╝ņØś ņĀĢļ░ĆļÅäļÅä ļåÆņØ╝ ņłś ņ׳Ļ│Ā ļŗżņ¢æĒĢ£ ļČäņäØļÅä Ļ░ĆļŖźĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ļ¦ÄņØäņłśļĪØ ņóŗļŗż.
ņŚ░ĻĄ¼ņŻ╝ņĀ£ ņäĀņĀĢ ļŗ©Ļ│äņŚÉņä£ ļ®öĒāĆļČäņäØņØ┤ Ļ░ĆļŖźĒĢśĻ▓ĀļŗżĻ│Ā ĒīÉļŗ©ļÉśļ®┤ ņŚ░ĻĄ¼ņ¦łļ¼Ė ņĀ£ĻĖ░ ļŗ©Ļ│äļĪ£ ļäśņ¢┤Ļ░äļŗż. ņŚ░ĻĄ¼ņ¦łļ¼ĖņØĆ Ļ░ĆļŖźĒĢ£ ĻĄ¼ņ▓┤ņĀüņ£╝ļĪ£ ņäżņĀĢĒĢśļŖö Ļ▓āņØ┤ ņóŗņØĆļŹ░, ņØ╝ļ░śņĀüņ£╝ļĪ£ ļŗżņØī ļäżĻ░Ćņ¦Ć ĒŖ╣ņä▒, ņ”ē, ļīĆņāü(population), ņ╣śļŻī Ēś╣ņØĆ ņżæņ×¼(intervention), ļ╣äĻĄÉĻĄ░(comparator), Ļ▓░Ļ│╝(outcomes)ļź╝ ĒżĒĢ©ĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ņśüļ¼Ė ļ©Ėļ”¼ĻĖĆņ×Éļź╝ ļö░ņä£ PICO ĒśĢņŗØņØ┤ļØ╝Ļ│Ā ļČĆļźĖļŗż[1]. ņśłļź╝ ļōżņ¢┤ ņŚ░ĻĄ¼ ņŻ╝ņĀ£ļź╝ ŌĆ£ņäżĻĘ╝ļČĆ ņłśņłĀņØĆ ĒÅÉņćäņä▒ņłśļ®┤ļ¼┤ĒśĖĒØĪņ”Ø ņ╣śļŻīņŚÉ ĒÜ©Ļ│╝ņĀüņØĖĻ░Ć?ŌĆØļØ╝ ņĀĢĒĢ┤ņĪīņ£╝ļ®┤, PICOļŖö ŌĆ£ņä▒ņØĖ ņżæņ”Ø ĒÅÉņćäņä▒ņłśļ®┤ļ¼┤ĒśĖĒØĪņ”Ø ĒÖśņ×É(P)ņŚÉņä£ ņäżĻĘ╝ļČĆ ņłśņłĀņØĆ(I)ņØĆ sham ņłśņłĀ(C)ņŚÉ ļ╣äĒĢ┤ ņä£ ļ¼┤ĒśĖĒØĪ-ņĀĆĒśĖĒØĪ ņ¦Ćņłśļź╝ Ļ▓ĮĻ░É(O)ņŗ£Ēé¼ ņłś ņ׳ļŖöĻ░Ć?ŌĆØ ņĀĢļÅäĻ░Ć ļÉĀ Ļ▓āņØ┤ļŗż. PICOļź╝ ĻĖ░ņżĆņ£╝ļĪ£ ļģ╝ļ¼ĖņØś ņäĀņĀĢĻĖ░ņżĆņØ┤ ņĀĢĒĢ┤ņ¦ĆĻ▓īļÉśļ»ĆļĪ£ ņŗĀņżæĒĢśĻ▓ī ļ¦īļōżņ¢┤ņĢ╝ ĒĢ£ļŗż.
Ļ┤ĆļĀ© ļ¼ĖĒŚīņØś ņ▓┤Ļ│äņĀü Ļ▓Ćņāē
ņØ┤ņĀ£ ļ│ĖĻ▓®ņĀüņ£╝ļĪ£ ĒĢäņÜöĒĢ£ ļģ╝ļ¼ĖņØä ņ░ŠļŖö Ļ▓Ćņāēļŗ©Ļ│äņØ┤ļŗż. PubMedļź╝ ĻĖ░ļ│Ėņ£╝ļĪ£ ņé¼ņÜ®ĒĢśņ¦Ćļ¦ī, Embase ļō▒ņØś ņ£ĀļŻī ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżļéś Google scholarļÅä ņ£ĀņÜ®ĒĢśļŗż. ņŚ░ĻĄ¼ņ×ÉĻ░Ć ņØśļÅäĒĢśļŖö ņĀĢĒÖĢĒĢ£ Ļ▓ĆņāēņØä ņ£äĒĢ┤ņä£ļŖö medical subject headings(MeSH) termņØä ņé¼ņÜ®ĒĢśļŖö Ļ▓āņØ┤ ņ£Āļ”¼ĒĢ£ļŹ░, MeSHļ×Ć ļ»ĖĻĄŁ ĻĄŁļ”ĮņØśĒĢÖļÅäņä£Ļ┤ĆņŚÉņä£ ņāØņØśĒĢÖ ļ░Å Ļ▒┤Ļ░ĢĻ┤ĆļĀ© ņĀĢļ│┤ņÖĆ ļ¼ĖĒŚīļōżņØä ļČäļźśĒĢśĻ│Ā Ļ▓ĆņāēĒĢśĻĖ░ ņ£äĒĢ┤ ņé¼ņÜ®ĒĢśļŖö Ļ│äņĖĄĒÖöļÉ£ ĒåĄņĀ£ ņØśĒĢÖņÜ®ņ¢┤ ļČäļźśņ¦æņØ┤ļŗż. ļśÉĒĢ£ ņ×ģļĀźņ░ĮņŚÉ ņøÉĒĢśļŖö Ļ▓Ćņāēņ¢┤ļź╝ ņ×ģļĀźĒĢĀ ļĢī, ņĢäļלņÖĆ Ļ░ÖņØ┤ ļ¬ćĻ░Ćņ¦Ć ĻĖ░ĒśĖļź╝ ņé¼ņÜ®ĒĢśļ®┤ ļŗżņ¢æĒĢ£ Ļ▓ĆņāēņØ┤ Ļ░ĆļŖźĒĢśļŗż[4].
ŌĆóŌĆ£ ŌĆ£: ļæÉĻ░£ņØś Ļ▓Ćņāēņ¢┤ļź╝ ĒĢśļéśļĪ£ ļ¼Čņ¢┤ņä£ Ļ▓Ćņāē (ņśł: ŌĆ£allergic rhinitisŌĆØ)
ŌĆóAND: ņĢ×Ļ│╝ ļÆżņØś Ļ▓Ćņāēņ¢┤ļź╝ ļ¬©ļæÉ ĒżĒĢ©ĒĢ£ Ļ▓ĮņÜ░ļ¦ī Ļ▓Ćņāē(ņśł: lung AND cancer)
ŌĆóOR: ņĢ×Ļ│╝ ļÆżņØś Ļ▓Ćņāēņ¢┤ ņżæ ĒĢśļéśļØ╝ļÅä ĒżĒĢ©ĒĢ£ Ļ▓ĮņÜ░ Ļ▓Ćņāē(ņśł: lung OR cancer)
ŌĆóNOT: ņĢ×ņØś Ļ▓Ćņāēņ¢┤ļŖö ĒżĒĢ©ĒĢśĻ│Ā ļÆżņØś Ļ▓Ćņāēņ¢┤ļŖö ĒżĒĢ©ĒĢśņ¦Ć ņĢŖļŖö Ļ▓ĮņÜ░ Ļ▓Ćņāē(ņśł: lung NOT cancer)
ŌĆó( ): Ļ┤äĒśĖņĢłņØś ļé┤ņÜ®ņØä ļ©╝ņĀĆ ņ▓śļ”¼ *: * ņĢ×ņŚÉ ņ£äņ╣śĒĢ£ ņ¢┤ļæÉļź╝ ĒżĒĢ©ĒĢ£ ļ¬©ļōĀ ļŗ©ņ¢┤ Ļ▓Ćņāē(ņśł: allerg*ļĪ£ Ļ▓ĆņāēĒĢśļ®┤ allergic, allergen, allergy ļō▒ņØä ļ¬©ļæÉ Ļ▓Ćņāē)
ŌĆó[ ]: Ļ▓Ćņāēņ¢┤ņŚÉ ņåŹņä▒ņØä ļČĆņŚ¼(ņśł: Smith A [au] ņĀĆņ×É Ļ▓Ćņāē, ŌĆ£allergic rhinitisŌĆØ [ti] ņĀ£ļ¬® Ļ▓Ćņāē)
ļśÉĒĢ£ Ļ╝Ł ņČ£Ļ░äļÉ£ ļģ╝ļ¼Ėļ¦ī ņĢäļŗłļØ╝ ņČ£ņ▓śĻ░Ć ļČäļ¬ģĒĢ£ ņ×ÉļŻīĻ░Ć ņ׳ļŗżļ®┤ ņØ┤ ļśÉĒĢ£ ņé¼ņÜ® Ļ░ĆļŖźĒĢśļŗż. ļśÉĒĢ£ ņ×Ŗņ¦Ć ļ¦ÉņĢäņĢ╝ ĒĢĀ Ļ▓ĆņāēĻ│╝ņĀĢņØ┤ Ļ┤ĆļĀ© ļģ╝ļ¼ĖņØś ņ░ĖĻ│Āļ¼ĖĒŚī ļ¬®ļĪØ Ļ▓ĆņāēņØ┤ļŗż. ņŚ░ĻĄ¼ņŻ╝ņĀ£ņØś review ļģ╝ļ¼ĖņØ┤ļéś ņŻ╝ņÜö ļģ╝ļ¼ĖņØś ņ░ĖĻ│Āļ¼ĖĒŚīņØä Ļ▓ĆņāēĒĢśļŗż ļ│┤ļ®┤ ļ»Ėņ▓ś ļ░£Ļ▓¼ĒĢśņ¦Ć ļ¬╗ĒĢ£ ļģ╝ļ¼ĖņØä ņ░ŠņØä ņłś ņ׳ļŖö Ļ▓ĮņÜ░Ļ░Ć ļ¦ÄĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. Preferred reporting items for systematic reviews and metaanalyses(PRISMA)ļŖö ļģ╝ļ¼ĖņØś Ļ▓Ćņāēļŗ©Ļ│äņŚÉņä£ ņĄ£ņóģņĀüņØĖ ņäĀņĀĢ Ļ│╝ņĀĢĻ╣īņ¦Ć ĻĖ░ņłĀĒĢśļŖö ļŗżņØ┤ņ¢┤ĻĘĖļשņ£╝ļĪ£ ļīĆļČĆļČäņØś ļ®öĒāĆļČäņäØņŚÉ ĒĢäņłśņĀüņ£╝ļĪ£ ņÜöĻĄ¼ĒĢśļŖö ņé¼ĒĢŁņØ┤ļ»ĆļĪ£, ņŚ░ĻĄ¼ņ×ÉļōżļÅä ņØ┤ ņĀłņ░©ņŚÉ ļö░ļØ╝ ņŗ£Ē¢ēĒĢśĻ│Ā ĻĘĖ Ļ▓░Ļ│╝ļź╝ ņĀ£ņČ£ĒĢ┤ņĢ╝ ĒĢ£ļŗż(Fig. 1) [1,2].
ņŚ░ĻĄ¼ņØś ņ¦ł Ļ▓Ćņ”Ø ļ░Å ļŹ░ņØ┤Ēä░ ņĮöļö®
ĻĘĖ ļŗżņØīņØĆ ņĄ£ņóģ ņäĀļ░£ļÉ£ ļģ╝ļ¼ĖļōżņØś ņ¦ł ĒÅēĻ░ĆņØ┤ļŗż. ņØ┤ļŖö Ļ░ü ļģ╝ļ¼ĖņØś risk of biasļź╝ ĒÅēĻ░ĆĒĢśĻĖ░ ņ£äĒĢ┤ ņŗ£Ē¢ēļÉśļŖöļŹ░ ņŚ░ĻĄ¼ņØś ĒśĢņŗØņŚÉ ļö░ļØ╝ ņĀüĒĢ®ĒĢ£ ĒÅēĻ░ĆļÅäĻĄ¼ļź╝ ņé¼ņÜ®ĒĢ┤ ņŗ£Ē¢ēĒĢśĻ▓ī ļÉ£ļŗż. ļŹ░ņØ┤Ēä░ ņĮöļö® Ļ│╝ņĀĢņŚÉļŖö ņØ╝ļ░śņĀüņ£╝ļĪ£ ņĀ£1ņĀĆņ×É ņØ┤ļ”ä, ņČ£Ļ░ä ņŚ░ļÅä, Ēæ£ļ│ĖņØś ĒŖ╣ņä▒, ņ╣śļŻīņØś ĒŖ╣ņä▒, ņŚ░ĻĄ¼ņØś ņ£ĀĒśĢ, ņŚ░ĻĄ¼ņ¦æļŗ©ņØś ļ░░ņĀĢ ļ░®ļ▓Ģ, ņĖĪņĀĢļÅäĻĄ¼, ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņŚÉ ļīĆĒĢ£ ņĀĢļ│┤ļź╝ ņ×ģļĀźĒĢśĻ▓ī ļÉ£ļŗż[1].
ļŹ░ņØ┤Ēä░ ļČäņäØ
Forest plotņØś ņØ┤ĒĢ┤
ļ®öĒāĆļČäņäØņØś Ļ▓░Ļ│╝ļŖö ļ¬©ļæÉ Forest plotņ£╝ļĪ£ ļ¦īļōżņ¢┤ņ¦ĆĻĖ░ ļĢīļ¼ĖņŚÉ ņØ┤ļź╝ ņל ņØ┤ĒĢ┤ĒĢśļŖö Ļ▓āņØ┤ ĒĢäņłśņĀüņØĖļŹ░, Ļ░ü Ļ░£ļ│ä ņŚ░ĻĄ¼ņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░(effect size), ĒåĄĻ│äņĀü ņ£ĀņØśņä▒, Ļ░Ćņżæņ╣śņÖĆ ĒĢ©Ļ╗ś Ļ░£ļ│ä ņŚ░ĻĄ¼ļź╝ ņóģĒĢ®ĒĢ£ ņĀäņ▓┤ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņÖĆ ĒåĄĻ│äņĀü ņ£ĀņØśņä▒ņØä ņ”ēņŗ£ ĒīīņĢģĒĢĀ ņłś ņ׳ĻĖ░ ļĢīļ¼ĖņØ┤ļŗż.
ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļŖö ņ╣śļŻīņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░ ļśÉļŖö ļ│Ćņłś Ļ░ä Ļ┤ĆĻ│äņØś Ēü¼ĻĖ░ļź╝ Ēæ£ĒśäĒĢ£ Ļ░Æņ£╝ļĪ£ ļ®öĒāĆļČäņäØņŚÉņä£ ļČäņäØ ļŗ©ņ£äņŚÉ ĒĢ┤ļŗ╣ĒĢ£ļŗż. ļ®öĒāĆļČäņäØņŚÉņä£ ĒØöĒ׳ ņé¼ņÜ®ļÉśļŖö ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņØś ņ£ĀĒśĢņØĆ 1) Ēæ£ņżĆĒÖöļÉ£ ĒÅēĻĘĀ ņ░©ņØ┤, 2) ļæÉ ņ¦æļŗ©ņØś ļ╣äņ£©, 3) ļæÉ ļ│Ćņłś Ļ░äņØś ņāüĻ┤Ć Ļ┤ĆĻ│äņØ┤ļŗż. ļ®öĒāĆļČäņäØņŚÉņä£ļŖö ņÜ░ņäĀ Ļ░£ļ│ä ņŚ░ĻĄ¼ņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļź╝ Ļ│äņé░ĒĢśĻ│Ā, Ļ░£ļ│ä ņŚ░ĻĄ¼ ņé¼ņØ┤ņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░ ņØ╝Ļ┤Ćņä▒ņØä Ļ▓ĆĒåĀĒĢśļ®░, ļ¦łņ¦Ćļ¦ēņ£╝ļĪ£ ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░(Ļ░£ļ│ä ņŚ░ĻĄ¼ņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņÖĆ Ļ░Ćņżæņ╣ś Ļ│▒ņØś ĒĢ®ņØä Ļ░Ćņżæņ╣ś ĒĢ®ņ£╝ļĪ£ ļéśļłł Ļ░Æ)ļź╝ ņé░ņČ£ĒĢśņŚ¼ ņ£ĀņØśņä▒ņØä Ļ▓ĆĒåĀĒĢ£ļŗż. Ļ░£ļ│ä ņŚ░ĻĄ¼ņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņÖĆ ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļź╝ ĻĄ¼ĒĢśļŖö ņ×ÉņäĖĒĢ£ Ļ│ĄņŗØņØĆ ļ│Ė ņóģņäżņØś ļ▓öņ£äļź╝ ļ▓Śņ¢┤ļéś ņāØļץĒĢśņśĆļŗż[1,2].
Forest plotņŚÉņä£ ņé¼Ļ░üĒśĢņØś ņ£äņ╣śļŖö Ļ░£ļ│ä ņŚ░ĻĄ¼ņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņÖĆ ļ░®Ē¢ź(+ Ēś╣ņØĆ -)ņØä ļéśĒāĆļé┤Ļ│Ā, ņé¼Ļ░üĒśĢņØś Ēü¼ĻĖ░ļŖö Ļ░Ćņżæņ╣ś(ņé¼Ļ░üĒśĢņØś Ēü¼ĻĖ░Ļ░Ć Ēü┤ņłśļĪØ Ļ░Ćņżæņ╣śĻ░Ć ņ╗żņ¦ĆļŖö Ļ▓āņØä ņØśļ»ĖĒĢśņŚ¼ ņØ╝ļ░śņĀüņ£╝ļĪ£ ļČäņé░ņØś ņŚŁņłś), ļŗżņØ┤ņĢäļ¬¼ļō£ļŖö ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļź╝ ļéśĒāĆļéĖļŗż. Ļ░ü ņŚ░ĻĄ¼ņØś ĒåĄĻ│äņĀü ņ£ĀņØśņä▒ņØĆ Ļ░ĆļĪ£ļ¦ēļīĆņØś ĻĖĖņØ┤ļĪ£ Ēæ£ņŗ£ļÉśļŖöļŹ░ ņŻ╝ļĪ£ 95% ņŗĀļó░ĻĄ¼Ļ░äņØä ņØśļ»ĖĒĢśļ®░, ņØ┤ ĻĄ¼Ļ░äņØ┤ ļäÆņØä ņłśļĪØ ĻĘĖ ņŚ░ĻĄ¼ņØś Ļ░Ćņżæņ╣śļŖö ņ×æņĢäņ¦äļŗż.
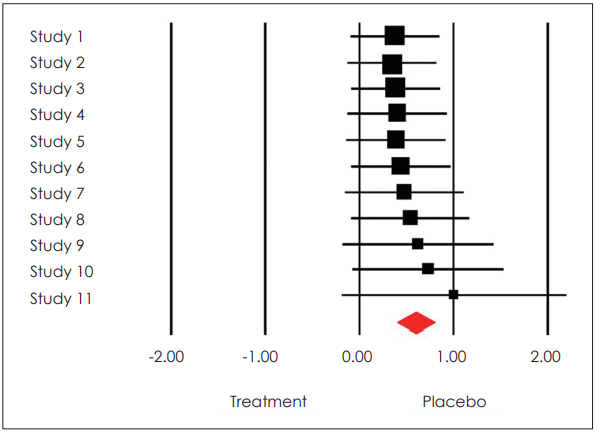
ņśłņŗ£ļĪ£ ļōĀ Forest plot (Fig. 2)ņŚÉņä£ ļ│┤ļ®┤ Study 1 Ļ▓ĮņÜ░ ņé¼Ļ░üĒśĢņØś ņ£äņ╣śĻ░Ć 0ļ│┤ļŗż ņ×æņØĆ Ļ││ņŚÉ ņ£äņ╣śĒĢśĻ│Ā ņ׳ņ£╝ļ®░, Ļ░ĆļĪ£ļ¦ēļīĆņØś ļ▓öņ£äļÅä 0ņØä ĒżĒĢ©ĒĢśņ¦Ć ņĢŖĻĖ░ ļĢīļ¼ĖņŚÉ, drug AĻ░Ć ņ£äņĢĮņŚÉ ļ╣äĒĢ┤ ņØśļ»Ėņ׳Ļ▓ī ļ¬Ėļ¼┤Ļ▓īļź╝ ņżäņØ┤ļŖö ĒÜ©Ļ│╝Ļ░Ć ņ׳ņŚłļŗżĻ│Ā ĒĢĀ ņłś ņ׳ļŗż. ļ░śļ®┤ Study 4ņØś Ļ▓ĮņÜ░ ņé¼Ļ░üĒśĢņØś ņ£äņ╣śĻ░Ć 0ļ│┤ļŗż ņ×æņØĆ Ļ││ņŚÉ ņ£äņ╣śĒĢśĻ│Ā ņ׳ņ¦Ćļ¦ī, Ļ░ĆļĪ£ļ¦ēļīĆņØś ļ▓öņ£äĻ░Ć 0ņØä ĒżĒĢ©ĒĢśĻ│Ā ņ׳ņ¢┤ drug AĻ░Ć ņ£äņĢĮņŚÉ ļ╣äĒĢ┤ ņØśļ»Ėņ׳Ļ▓ī ļ¬Ėļ¼┤Ļ▓īļź╝ ņżäņśĆļŗżĻ│Ā ĒĢĀ ņłśļŖö ņŚåĻ▓Āļŗż. ļæÉ ņŚ░ĻĄ¼ļź╝ ļ╣äĻĄÉĒĢ┤ ļ│┤ļ®┤ Study 1ņØś Ļ▓░Ļ│╝ļŖö ĒåĄĻ│äņĀü ņØśļ»ĖĻ░Ć ņ׳ņŚłĻ│Ā, Study 4ņØś Ļ▓░Ļ│╝ļŖö ņØśļ»ĖĻ░Ć ņŚåņŚłņ¦Ćļ¦ī, Ļ░Ćņżæņ╣śļŖö Study 4Ļ░Ć Ēü¼ĻĖ░ ļĢīļ¼ĖņŚÉ ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņŚÉļŖö ļŹö Ēü░ ņśüĒ¢źņØä ņżĆļŗż. ļ¬©ļōĀ ņŚ░ĻĄ¼ļōżņØś ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļź╝ ņØśļ»ĖĒĢśļŖö ļŗżņØ┤ņĢäļ¬¼ļō£ņØś Ļ╝Łņ¦ĆņĀÉņØ┤ 0ļ│┤ļŗż ņ×æņØĆ Ļ▓āņ£╝ļĪ£ ļ│┤ņĢä drug AĻ░Ć ņ£äņĢĮņŚÉ ļ╣äĒĢ┤ ļ¬Ėļ¼┤Ļ▓īļź╝ ņżäņØ┤ĻĖ░ļŖö ĒĢśņ¦Ćļ¦ī 0ņØä ĒżĒĢ©ĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ĒåĄĻ│äņĀü ņØśļ»ĖļŖö ņŚåļŗż.
Fixed-effect modelĻ│╝ Random-effect model
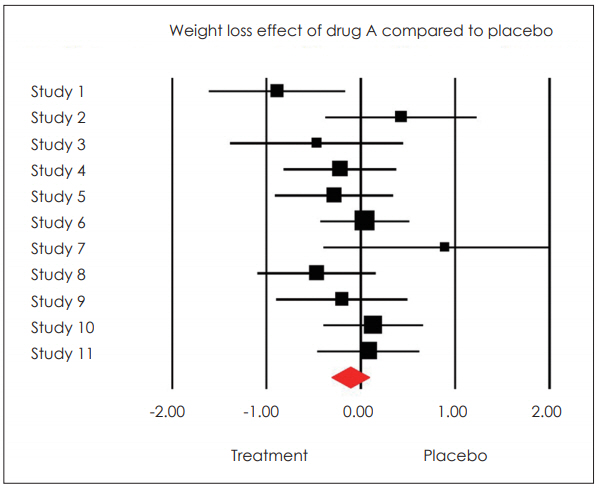
ļ®öĒāĆļČäņäØņŚÉņä£ ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļź╝ Ļ│äņé░ĒĢśļŖö ļ░®ļ▓ĢņØĆ Fixed-effect modelĻ│╝ Random-effect modelņØ┤ ņ׳ļŗż. ļæÉ ļ░®ļ▓ĢņØś Ļ░Ćņן ĒĢĄņŗ¼ņĀüņØĖ ņ░©ņØ┤ļŖö Fixed-effect modelņØś Ļ▓ĮņÜ░ Ļ░ü ņŚ░ĻĄ¼ļōżņØ┤ ļÅÖņØ╝ĒĢ£ ļ¬©ņ¦æļŗ©ņØä Ļ│Ąņ£ĀĒĢśĻ│Ā ņ׳ļŗżĻ│Ā Ļ░ĆņĀĢĒĢśļŖö Ļ▓āņØ┤Ļ│Ā Random-effect modelņØĆ Ļ░ü ņŚ░ĻĄ¼ļōżņØś ļ¬©ņ¦æļŗ©ņØ┤ ņä£ļĪ£ ļŗżļź┤ļŗżĻ│Ā Ļ░ĆņĀĢĒĢśļŖö Ļ▓āņØ┤ļŗż[1,2]. ņĀäņ×ÉņØś Ļ▓ĮņÜ░ ņŚ░ĻĄ¼ļōżņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░Ļ░Ć ļÅÖņØ╝ĒĢśĻ│Ā ņŚ░ĻĄ¼ļōż ņé¼ņØ┤ņØś ļČäņé░ņØä 0ņ£╝ļĪ£ Ļ│äņé░ĒĢśļ»ĆļĪ£ ņĀĢļ░Ćņä▒ņØ┤ ļåÆņĢäņ¦ĆĻ│Ā ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņØś ļ▓öņ£äĻ░Ć ņóüļŗż. ļ░śļ®┤ Ēøäņ×ÉņØś Ļ▓ĮņÜ░ ņŚ░ĻĄ¼ļōżņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░Ļ░Ć ļŗżļź┤Ļ│Ā ņŚ░ĻĄ¼ļōż ņé¼ņØ┤ņŚÉ ļČäņé░ļÅä ņØĖņĀĢĒĢśļ»ĆļĪ£ ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņØś ļ▓öņ£äĻ░Ć Ēø©ņö¼ ņ╗żņ¦ĆĻ▓ī ļÉ£ļŗż[1,2]. ļŹö ņ×ÉņäĖĒĢ£ ļæÉ ļ░®ļ▓ĢņØś ņ░©ņØ┤ļŖö ņĢäļל Ēæ£ņÖĆ ĻĘĖļ”╝ņØä ņ░ĖņĪ░ĒĢśĻĖ░ ļ░öļ×Ćļŗż(Fig. 3, Table 1).
ļ®öĒāĆļČäņäØņŚÉņä£ļŖö ĒØöĒ׳ ņŚ░ĻĄ¼ļōżņØś ļÅÖņ¦łņä▒ņŚÉ ĻĘ╝Ļ▒░ĒĢ┤ņä£ ļÅÖņ¦łņä▒ņØ┤ ļåÆņ£╝ļ®┤ Fixed-effect-modelņØä, ļé«ņ£╝ļ®┤ Random-effect modelņØä ņé¼ņÜ®ĒĢśļŖöļŹ░, ņØ┤ļŖö ņלļ¬╗ļÉ£ Ļ▓āņØ┤ļŗż. ņÖ£ļāÉĒĢśļ®┤ ļ¬©ĒśĢņØś ņäĀĒāØņØĆ ņŚ░ĻĄ¼ņ×ÉĻ░Ć ņŚ░ĻĄ¼ņØś ĒŖ╣ņä▒, ņ”ē ņŚ░ĻĄ¼ ļīĆņāü, ņ╣śļŻī ļ░®ļ▓Ģ, ņŚ░ĻĄ¼ ĒÖśĻ▓Į ļō▒ņØä ĒīīņĢģĒĢ£ Ēøä Ļ░£ļģÉņĀü ņØ┤ĒĢ┤ņŚÉ ĻĖ░ņ┤łĒĢ┤ņä£ ņØ┤ļŻ©ņ¢┤ņ¦ĆļŖö Ļ▓āņØ┤ņ¦Ć ļÅÖņ¦łņä▒ņŚÉ ļö░ļØ╝ Ļ▓░ņĀĢļÉśļŖö ņé¼ĒĢŁņØ┤ ņĢäļŗłĻĖ░ ļĢīļ¼ĖņØ┤ļŗż[1].
ļŗżņżæĻ▓░Ļ│╝ ļČäņäØ
ļ®öĒāĆļČäņäØņŚÉņä£ļŖö Ļ▓░Ļ│╝Ļ░Ć ļŗżļźĖ Ļ░ÆņØĖ Ļ▓ĮņÜ░ņŚÉļÅä ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļź╝ ļČäņäØĒĢĀ ņłś ņ׳ļŗż. ņśłļź╝ ļōżņ¢┤ ņāłļĪ£ņÜ┤ ļČĆļ╣äļÅÖ ļé┤ņŗ£Ļ▓Į ņłśņłĀļ▓ĢņŚÉ ļīĆĒĢ£ ņŚ░ĻĄ¼ļōżņØä ļ®öĒāĆļČäņäØ ĒĢśļŖöļŹ░ ņØ╝ļČĆ ņŚ░ĻĄ¼ļōżņØĆ Ļ▓░Ļ│╝Ļ░Æņ£╝ļĪ£ Visual Analogue ScaleņØä ņé¼ņÜ®ĒĢśņśĆĻ│Ā, ļéśļ©Ėņ¦ĆļŖö SinoNasal Outcome Test-22ļź╝ ņé¼ņÜ®ĒĢ£ Ļ▓ĮņÜ░ļØ╝ļÅä ĒĢ®ņ│Éņä£ ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļź╝ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗżļŖö ņØśļ»ĖļĪ£ ņØ┤ļź╝ ļŗżņżæĻ▓░Ļ│╝ ļČäņäØņØ┤ļØ╝Ļ│Ā ĒĢ£ļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ▓░ĒĢ®ņØ┤ Ļ░ĆļŖźĒĢ£ ņØ┤ņ£ĀļŖö ļ®öĒāĆļČäņäØņŚÉņä£ļŖö Ļ░ü ņŚ░ĻĄ¼ņØś Ļ▓░Ļ│╝Ļ░ÆņØ┤ Ēæ£ņżĆĒÖöļÉ£ ĒÅēĻĘĀ ņ░©ņØ┤ļĪ£ ļ│ĆĒÖśļÉśņ¢┤ Ļ│äņé░ļÉśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ļŗżņżæĻ▓░Ļ│╝ ļČäņäØņØä ņ£äĒĢ┤ņä£ļŖö ļæÉĻ░£ņØś ļŗżļźĖ Ļ▓░Ļ│╝Ļ░Æ ņé¼ņØ┤ņŚÉ ņāüĻ┤ĆĻ┤ĆĻ│äļź╝ ņ×äņØśļĪ£ Ļ░ĆņĀĢĒĢ┤ņä£ ņāüĻ┤ĆĻ│äņłśļź╝ ņ¦ĆņĀĢĒĢ┤ņĢ╝ ĒĢśļŖöļŹ░(ņśł: Visual Analogue ScaleĻ│╝ Sino-Nasal Outcome Test-22ņØś ņāüĻ┤ĆĻ┤ĆĻ│ä). ņØ┤ļĢī ņāüĻ┤ĆĻ│äņłśļź╝ 0ņØ┤ļØ╝Ļ│Ā Ļ░ĆņĀĢĒĢśļ®┤ ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņØś ļČäņé░ņØ┤ ņ×æĻ▓ī Ļ│äņé░ļÉśņ¢┤ 1ņóģ ņśżļźśņØś ĒÖĢļźĀņØ┤ ņ╗żņ¦ĆĻ▓ī ļÉ£ļŗż[1].
ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņØś ņØ┤ņ¦łņä▒
ļ®öĒāĆļČäņäØņŚÉ ņé¼ņÜ®ļÉ£ ņŚ░ĻĄ¼ļōżņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░ Ļ░ä ņ░©ņØ┤ļź╝ ņØ┤ņ¦łņä▒(heterogeneity)ņØ┤ļØ╝Ļ│Ā ĒĢ£ļŗż. ņØ┤ņ¦łņä▒ņØś ņĀĢļÅäļŖö Forest plotņØä ĒåĄĒĢ┤ ņŗ£Ļ░üņĀüņ£╝ļĪ£ ĒÖĢņØĖņØ┤ Ļ░ĆļŖź ĒĢśņ¦Ćļ¦ī, ļŗżņ¢æĒĢ£ ĒåĄĻ│äņ╣śļź╝ ĒåĄĒĢ┤ Ļ░ØĻ┤ĆņĀüņ£╝ļĪ£ļÅä ĒÖĢņØĖņØ┤ Ļ░ĆļŖźĒĢśļŗż. ļ®öĒāĆļČäņäØņØś ņØ┤ņ¦łņä▒ Ļ▓Ćņ”ØņŚÉ ņ×ÉņŻ╝ ņé¼ņÜ®ļÉśļŖö ĒåĄĻ│äņ╣śļŖö ļŗżņØīĻ│╝ Ļ░Öļŗż[1,2].
ŌĆó QĻ░Æ: Ļ┤Ćņ░░ļÉ£ ņĀäņ▓┤ ļČäņé░Ļ░Æņ£╝ļĪ£ ņŗżņĀ£ ļČäņé░Ļ│╝ Ēæ£ņ¦æ ņśżņ░©ļź╝ ļŹöĒĢ£ Ļ░ÆņØ┤ļŗż. ņØ┤ Ļ░ÆņØä ĻĘ╝Ļ▒░ļĪ£ ļÅÖņ¦łņä▒ Ļ▓Ćņ”ØņØä ņŗ£Ē¢ēĒĢśļŖöļŹ░, pĻ░ÆņØ┤ 0.10ļ│┤ļŗż ņ×æņØĆ Ļ▓ĮņÜ░ ņŚ░ĻĄ¼Ļ░äņØś ņØ┤ņ¦łņä▒ņØ┤ ņ׳ļŗżĻ│Ā ĒīÉļŗ©ĒĢ£ļŗż.
ŌĆó T2(tau squared): ņŗżņĀ£ ņä£ļĪ£ ļŗżļźĖ ļ¬©ņ¦æļŗ© ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņŚÉ ņØśĒĢ£ ļČäņé░ņ£╝ļĪ£ ņŚ░ĻĄ¼ Ļ░ä ļČäņé░(ņŗżņĀ£ ļČäņé░)ņØä ņØśļ»ĖĒĢ£ļŗż. ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņØś ļ▓öņ£äļź╝ ĻĄ¼ĒĢśĻĖ░ ņ£äĒĢ┤ ņé¼ņÜ®ļÉ£ļŗż.
ŌĆó I2(I squared): ņ┤ØļČäņé░ņŚÉ ļīĆĒĢ£ ņŗżņĀ£ ņŚ░ĻĄ¼ Ļ░ä ļČäņé░ņØś ļ╣äņ£©ņØ┤ļŗż. 25% ņØ┤ĒĢśņØ┤ļ®┤ ņØ┤ņ¦łņä▒ņØ┤ ņ×æņØĆ Ļ▓āņ£╝ļĪ£, 50%ņØ┤ļ®┤ ņżæĻ░ä, 75% ņØ┤ņāüņØ┤ļ®┤ ļ¦żņÜ░ Ēü░ Ļ▓āņ£╝ļĪ£ ĒĢ┤ņäØĒĢ£ļŗż.
ņŻ╝ļĪ£ ļÅÖņ¦łņä▒ Ļ▓Ćņ”Ø pĻ░ÆņØ┤ 0.1 ņØ┤ĒĢśņØ┤Ļ│Ā I2Ļ░Ć 50% ņØ┤ņāüņØ┤ļ®┤ ņØ┤ņ¦łņä▒ņØ┤ ņāüļŗ╣ĒĢśļŗżĻ│Ā ĒīÉļŗ©ĒĢśļŗż. ĒśäņŗżņĀüņ£╝ļĪ£ ņØ┤ņ¦łņä▒ņØ┤ Ēü░ Ļ▓ĮņÜ░ Random-effect modelņØä, ĻĘĖļĀćņ¦Ć ņĢŖņØĆ Ļ▓ĮņÜ░ Fixed-effect modelņØä ņé¼ņÜ®ĒĢśĻ▓ī ļÉśļŖö Ļ▓ĮņÜ░Ļ░Ć ļ¦ÄņØĆļŹ░ ņ£äņŚÉņä£ ņäżļ¬ģĒĢśņśĆļō»ņØ┤ ņś¼ļ░öļźĖ ļ░®ļ▓ĢņØĆ ņĢäļŗłļŗż. ņØ┤ņ¦łņä▒ņØ┤ ņĀüņØĆ Ļ▓ĮņÜ░ļŖö ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļź╝ ņĀ£ņŗ£ĒĢśļŖö Ļ▓āņŚÉ ņ┤łņĀÉņØä ļæÉĻ▓ī ļÉśĻ│Ā, ņØ┤ņ¦łņä▒ņØ┤ Ēü░ Ļ▓ĮņÜ░ļŖö ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļ│┤ļŗżļŖö ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņØś ļČäņé░ņŚÉ ņ┤łņĀÉņØä ļæÉĻ│Ā ļČäņé░ņØś ņøÉņØĖņØä ņ░ŠļŖö ļģĖļĀźņØä ĒĢśĻ▓ī ļÉśļŖöļŹ░ ņØ┤ļź╝ ņĪ░ņĀł ĒÜ©Ļ│╝ ļČäņäØņØ┤ļØ╝Ļ│Ā ĒĢ£ļŗż[1].
ņĪ░ņĀł ĒÜ©Ļ│╝ ļČäņäØ
ļ®öĒāĆļČäņäØņŚÉņä£ ņĪ░ņĀł ĒÜ©Ļ│╝ ļČäņäØņØś ņØśļ»ĖļŖö ĒĢśņ£ä ņ¦æļŗ©Ļ░äņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░ ņ░©ņØ┤ļź╝ ĻĘ£ļ¬ģĒĢśĻ▒░ļéś(ĒĢśņ£äĻĘĖļŻ╣ ļČäņäØ, subgroup analysis), ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņŚÉ ņśüĒ¢źņØä ņŻ╝ļŖö ļ│Ćņłśļź╝ Ļ▓Ćņ”ØĒĢśļŖö Ļ▓āņØ┤ļŗż(meta-ANOVA Ēś╣ņØĆ meta-regression) [1].
ĒĢśņ£äĻĘĖļŻ╣ ļČäņäØņØĆ ņŚ░ĻĄ¼ļōż Ļ░äņØś ņØ┤ņ¦łņä▒ņØ┤ ņ×äņāüņĀüņØĖ ņøÉņØĖ(ņä▒, ņŚ░ļĀ╣, ņŚ░ĻĄ¼ļīĆņāüņØś ĒŖ╣ņä▒, ņĢĮļ¼╝ņØś ņ¢æņØ┤ļéś Ēł¼ņŚ¼ ĻĖ░Ļ░ä, ņ¦łļ│æņØś ņżæņ”ØļÅä, ņ¦äļŗ©ĻĖ░ņżĆ, Ļ▓░Ļ│╝ļ│ĆņłśņØś ņĀĢņØś, ņČöņĀü ĻĖ░Ļ░ä ļō▒)ņØ┤ļéś ļ░®ļ▓ĢļĪĀņĀüņØĖ ļŗżņ¢æņä▒(ņŚ░ĻĄ¼ ļööņ×ÉņØĖĻ│╝ ņ¦ł, ļ¼┤ņ×æņ£ä ņäĀņĀĢ ņŚ¼ļČĆ, Ļ▓░Ļ│╝ ļČäņäØ ņ░©ņØ┤ ļō▒) ļō▒ņŚÉ ĻĖ░ņØĖĒĢ£ Ļ▓āņØĖņ¦Ćļź╝ ĒīīņĢģĒĢśĻ│Āņ×É ĒŖ╣ņä▒ņØ┤ ļ╣äņŖĘĒĢ£ ņŚ░ĻĄ¼ļōżņØä ņåīĻĘĖļŻ╣ņ£╝ļĪ£ ļ¦īļōżņ¢┤ ļČäņäØĒĢśļŖö ļ░®ļ▓ĢņØä ļ¦ÉĒĢ£ļŗż[5]. ĒĢśņ£äĻĘĖļŻ╣ ļČäņäØņØĆ ĒżĒĢ©ļÉśļŖö ņŚ░ĻĄ¼ņłśĻ░Ć ņ×æņĢä Ļ▓Ćņ”ØļĀźņØ┤ ļé«ņĢäņ¦Ćļ»ĆļĪ£ ĒĢ┤ņäØņŚÉ ņŗĀņżæĒĢ┤ņĢ╝ ĒĢśļ®░, ļČäņäØĻ▓░Ļ│╝ļŖö ņŚ░ĻĄ¼ņŻ╝ņĀ£ņŚÉ ļīĆĒĢ£ Ļ▓░ļĪĀņØä ļé┤ļ”¼ĻĖ░ ņ£äĒĢ£ Ļ▓āņØ┤ ņĢäļŗłļØ╝ ņØ┤ņ¦łņä▒ņØś ņøÉņØĖņØä ņ░ŠĻ│Ā ĒøäņåŹ ņŚ░ĻĄ¼ļź╝ ņ£äĒĢ£ ņāłļĪ£ņÜ┤ Ļ░ĆņäżņØä ņĀ£ņŗ£ĒĢśĻĖ░ ņ£äĒĢ┤ ņé¼ņÜ®ĒĢ┤ņĢ╝ ĒĢ£ļŗż[5].
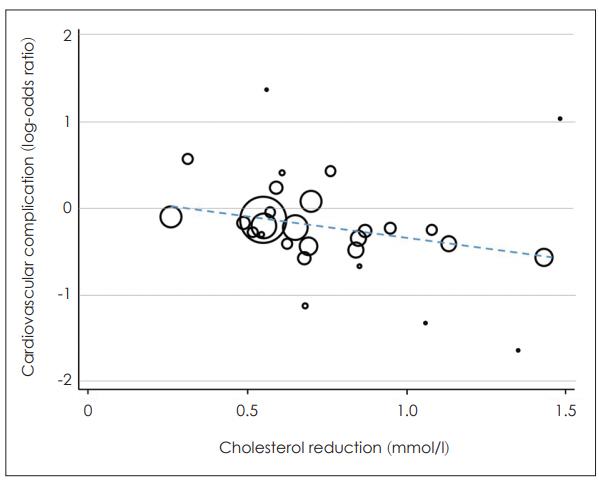
ņĪ░ņĀłļ│ĆņłśļŖö ļÅģļ”Įļ│ĆņłśņÖĆ ņóģņåŹļ│Ćņłś ņé¼ņØ┤ņŚÉ ņśüĒ¢źņØä ņŻ╝ļŖö ļ│ĆņłśļĪ£ ļ®öĒāĆļČäņäØņŚÉņä£ļŖö ņŚ░ĻĄ¼ ņłśņżĆņŚÉņä£ņØś ļ│Ćņłśļź╝ ņØśļ»ĖĒĢ£ļŗż. ņśłļź╝ ļōżņ¢┤ ņ¢┤ļ¢ż ņĢĮļ¼╝ņØś ņÜ®ļ¤ēņØä 50 mg ņé¼ņÜ®ĒĢ£ ņŚ░ĻĄ¼ļōżĻ│╝ 100 mg ņé¼ņÜ®ĒĢ£ ņŚ░ĻĄ¼ļōżņØä ļéśļłäņ¢┤ ļČäņäØĒ¢łļŹöļŗł ļæÉ ĻĄ░ņØś ĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņŚÉ ņ░©ņØ┤Ļ░Ć ņ׳ņŚłļŗżļ®┤ ņĢĮļ¼╝ņØś ņÜ®ļ¤ēņØ┤ ņ╣śļŻī ĒÜ©Ļ│╝ņŚÉ ņśüĒ¢źņØä ļ»Ėņ╣Ā Ļ░ĆļŖźņä▒ņØ┤ ņ׳ļŗżĻ░Ć ņØśņŗ¼ĒĢ┤ ļ│╝ ņłś ņ׳Ļ│Ā, ņØ┤ļĢī ņĢĮļ¼╝ņØś ņÜ®ļ¤ēņØĆ ļ®öĒāĆļČäņäØņØś ņĪ░ņĀłļ│ĆņłśĻ░Ć ļÉśļŖö Ļ▓āņØ┤ļŗż. ņĪ░ņĀłļ│ĆņłśĻ░Ć ļ▓öņŻ╝ĒśĢņØĖ Ļ▓ĮņÜ░ meta-ANOVAļź╝ ņé¼ņÜ®ĒĢśĻ│Ā ņŚ░ņåŹĒśĢņØĖ Ļ▓ĮņÜ░ meta-regressionņØä ņé¼ņÜ®ĒĢ£ļŗż(Fig. 4). ņØ┤ ļæÉ ļ░®ļ▓ĢņØĆ ņØ╝ļ░śņĀüņ£╝ļĪ£ ĒåĄĻ│äņŚÉņä£ ņé¼ņÜ®ĒĢśļŖö ANOVAļéś ĒÜīĻĘĆļČäņäØĻ│╝ļŖö ļŗżļź┤ļ®░, ņĪ░ņĀłļ│Ćņłśļŗ╣ ņĄ£ņåī 10Ļ░£ ņØ┤ņāüņØś ņŚ░ĻĄ¼Ļ░Ć ĒĢäņÜöĒĢśļŗż[1].
ņČ£Ļ░ä ņśżļźś ļČäņäØ
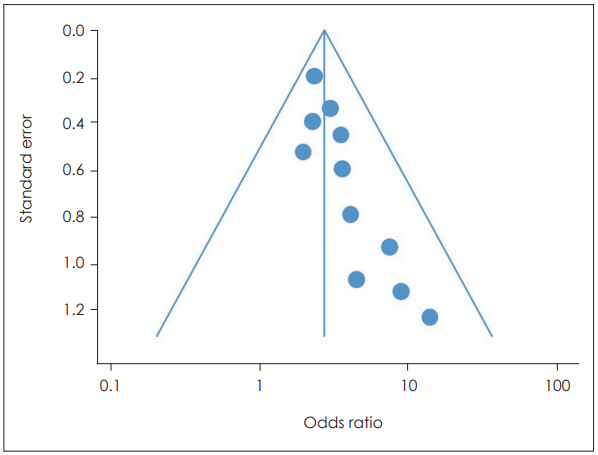
ļ®öĒāĆļČäņäØņŚÉļŖö ņŚ¼ļ¤¼ Ļ░Ćņ¦Ć ņśżļźś(bias)ņØś Ļ░ĆļŖźņä▒ņØ┤ ņ׳ņ¦Ćļ¦ī, Ļ░Ćņן ļ¼ĖņĀ£Ļ░Ć ļÉśļŖö Ļ▓āņØĖ ņČ£Ļ░ä ņśżļźś(publication bias)ņØ┤ļŗż[1,2]. ņČ£Ļ░ä ņśżļźśļ×Ć ņŚ░ĻĄ¼ņØś ņ¦łĻ│╝ Ļ┤ĆĻ│ä ņŚåņØ┤ ĒåĄĻ│äņĀüņ£╝ļĪ£ ņ£ĀņØśļ»ĖĒĢ£ Ļ▓░Ļ│╝ļź╝ ļÅäņČ£ĒĢ£ ņŚ░ĻĄ¼Ļ░Ć ņל ņČ£Ļ░äļÉśĻ│Ā ĻĘĖļĀćņ¦Ć ļ¬╗ĒĢ£ Ļ▓ĮņÜ░ ņČ£Ļ░äņØ┤ ņ¢┤ļĀżņÜ┤ ĒśäņŗżņØ┤ ļ®öĒāĆļČäņäØņØś Ļ▓░Ļ│╝ņŚÉ ņśüĒ¢źņØä ļ»Ėņ╣Ā ņłś ņ׳ļŗżļŖö ļ£╗ņØ┤ļŗż. ņČ£Ļ░ä ņśżļźśļĪ£ ņØĖĒĢ┤ ņÖ£Ļ│ĪļÉ£ Ēæ£ļ│ĖņŚÉņä£ ņŚ░ĻĄ¼ļōżņØä ļ¬©ņĢä ļČäņäØĒĢĀ Ļ▓ĮņÜ░ ņØ╝ļ░śņĀüņ£╝ļĪ£ Ļ│╝ļīĆņČöņĀĢņØ┤ ņØ╝ņ¢┤ļéśĻ▓ī ļÉśļŖöļŹ░, smallstudy effectļØ╝ ĒĢ£ļŗż. ņØ┤ļŖö 1) ĒåĄĻ│äņĀü ņ£ĀņØśņä▒ņŚÉ Ļ┤ĆĻ│äņŚåņØ┤ Ēæ£ļ│ĖņØ┤ Ēü░ ņŚ░ĻĄ¼ļŖö ņČ£Ļ░äļÉĀ Ļ░ĆļŖźņä▒ņØ┤ ļåÆĻ│Ā, 2) Ēæ£ļ│ĖņØ┤ ņżæĻ░ä Ēü¼ĻĖ░ņØĖ Ļ▓ĮņÜ░ ņČ£Ļ░äļÉśņ¦Ć ņĢŖņØä Ļ░ĆļŖźņä▒ņØ┤ ņ׳Ļ│Ā, 3) Ēæ£ļ│ĖņØ┤ ņ×æņØĆ Ļ▓ĮņÜ░ ĒÜ©Ļ│╝ Ēü¼ĻĖ░Ļ░Ć Ēü░ Ļ▓ĮņÜ░ļ¦ī ņČ£Ļ░äļÉĀ Ļ░ĆļŖźņä▒ņØ┤ ļåÆĻĖ░ ļĢīļ¼ĖņŚÉ ļ®öĒāĆļČäņäØņŚÉ ĒżĒĢ£ļÉ£ ņŚ░ĻĄ¼ ņżæ Ēæ£ļ│Ė Ēü¼ĻĖ░Ļ░Ć ņ×æņØĆ ņŚ░ĻĄ¼ļŖö ņāüļīĆņĀüņ£╝ļĪ£ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļŖö Ēü┤ Ļ░ĆļŖźņä▒ņØ┤ ļ¦ÄĻĖ░ ļĢīļ¼ĖņØ┤ļŗż[1]. ņØ┤ņŚÉ ļīĆĒĢ£ Ļ░ĆņäżņØä Ļ▓Ćņ”ØĒĢśļŖö Ļ▓āņØ┤ ņČ£Ļ░ä ņśżļźś ļČäņäØņØ┤ļŗż. Ļ░Ćņן ņ¦üĻ┤ĆņĀüņ£╝ļĪ£ ņĪ░ņé¼ĒĢ┤ ļ│╝ ņłś ņ׳ļŖö ļ░®ļ▓ĢņØĆ Forest plotņŚÉņä£ ņŚ░ĻĄ¼ļōżņØä Ļ░Ćņżæņ╣śļ│äļĪ£ ļéśņŚ┤ĒĢśĻ│Ā Ļ░Ćņżæņ╣śĻ░Ć ņ×æņØĆ ņŚ░ĻĄ¼ļōżņØ┤ ļīĆņ▓┤ņĀüņ£╝ļĪ£ ĒÜ©Ļ│╝ Ēü¼ĻĖ░Ļ░Ć Ēü░ņ¦Ć ĒÖĢņØĖĒĢśļŖö Ļ▓āņØ┤ļŗż(Fig. 5). ļŹö ļ¦ÄņØ┤ ņé¼ņÜ®ļÉśļŖö ļ░®ļ▓ĢņØĆ Funnel plotņØ┤ļŗż(Fig. 6). Ļ╣öļĢīĻĖ░ ļ¬©ņ¢æņØ┤ļØ╝Ļ│Ā ĒĢ┤ņä£ ļČÖņŚ¼ņ¦ä ņØ┤ļ”äņØĖļŹ░, ņłśĒÅēņČĢņØĆ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ļź╝ ņłśņ¦üņČĢņØĆ Ēæ£ņżĆņśżņ░©ļź╝ ņØśļ»ĖĒĢśļ®░, ļīĆĻ░üņäĀņØś Ļ░ü ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņØś 95% ņŗĀļó░ĻĄ¼Ļ░äņØ┤ļŗż[1]. ņØ╝ļ░śņĀüņ£╝ļĪ£ Ēæ£ļ│ĖņØ┤ Ēü░ ņŚ░ĻĄ¼ļōżņØ┤ ĻĘĖļלĒöä ņāüļŗ© ņżæņĢÖļČĆņŚÉ ļ¬░ļĀżņ׳Ļ│Ā, Ēæ£ļ│Ė Ēü¼ĻĖ░Ļ░Ć ņ×æņØĆ ņŚ░ĻĄ¼ļōżņØ┤ ĒĢśļŗ©ņŚÉ ļäōĻ▓ī ļČäĒżļÉśņ¢┤ ņ׳ļŗż. ņČ£Ļ░ä ņśżļźśĻ░Ć ņŚåļŖö Ļ▓ĮņÜ░ ņŚ░ĻĄ¼ļōżņØ┤ ņóīņÜ░ ļīĆņ╣Łņ£╝ļĪ£ ļČäĒżļÉśļŖöļŹ░ ļ╣äļīĆņ╣ŁņØ┤ļØ╝ļ®┤ ņČ£Ļ░ä ņśżļźśĻ░Ć ņØśņŗ¼ļÉ£ļŗż. ļ╣äļīĆņ╣ŁņŚÉ ļīĆĒĢ£ ĒåĄĻ│äņĀü ļČäņäØļÅä Ļ░ĆļŖźĒĢ£ļŹ░, ļīĆĒæ£ņĀüņ£╝ļĪ£ Egger testĻ░Ć ņ׳ļŗż[1]. ņØ┤ļŖö Ļ░ü ņŚ░ĻĄ¼ņØś ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņÖĆ Ēæ£ņżĆņśżņ░©ņÖĆņØś Ļ┤ĆĻ│äļź╝ ĒÜīĻĘĆņŗØņØä ņäżļ¬ģĒĢśļŖö ļ░®ļ▓ĢņØ┤ļŗż. Begg & Mazumdar testļÅä ņ׳ļŖöļŹ░, ņØ┤ļŖö ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņÖĆ ĻĘĖ ļČäņé░ Ļ░äņØś ņä£ņŚ┤ņāüĻ┤ĆĻ┤ĆĻ│äļź╝ ļ│┤ļŖö Ļ▓āņ£╝ļĪ£ Egger ļ░®ļ▓Ģļ│┤ļŗż Ļ▓Ćņ”ØļĀźņØ┤ ņĢĮĒĢ£ļŗż[1]. ņØ┤ļōż Ļ▓Ćņé¼ņŚÉņä£ pĻ░ÆņØ┤ 0.05 ņØ┤ĒĢśņØĖ Ļ▓ĮņÜ░ ņČ£Ļ░äņśżļźśĻ░Ć ņØśņŗ¼ļÉ£ļŗż ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ ņÖĖņŚÉļÅä ņČ£Ļ░ä ņśżļźśļź╝ ĒÅēĻ░ĆĒĢśļŖö ļ░®ļ▓Ģņ£╝ļĪ£ fail-safe N ļ░®ļ▓ĢņØ┤ ņ׳ļŖöļŹ░, ņØ┤ļŖö ņĀäņ▓┤ ĒÜ©Ļ│╝Ļ░Ć ņ£ĀņØśĒĢśņ¦Ć ņĢŖĻ▓ī ļÉśļĀżļ®┤ ņČöĻ░ĆņĀüņ£╝ļĪ£ ĒĢäņÜöĒĢ£ ņŚ░ĻĄ¼ņØś Ļ░»ņłśļź╝ ņØśļ»ĖĒĢśļŖöļŹ░ ļ░®ļ▓ĢĻ│╝ ĒīÉņĀĢņØś ļ¼ĖņĀ£ļĪ£ ņØĖĒĢ┤ ņĄ£ĻĘ╝ņŚÉļŖö ļ¦ÄņØ┤ ņé¼ņÜ®ļÉśņ¦Ć ņĢŖļŖöļŗż. ņČ£Ļ░ä ņśżļźśĻ░Ć ļ░£Ļ▓¼ļÉ£ Ļ▓ĮņÜ░ ņČ£Ļ░ä ņśżļźśļĪ£ ļ│┤ņĀĢĒĢśņŚ¼ ņāłļĪ£ņÜ┤ ĒÅēĻĘĀĻ░ÆņØä ĻĄ¼ĒĢśļŖö trim-and-fill ļ░®ļ▓ĢļÅä ņ׳ļŗż[1].
ļłäņĀü ļ®öĒāĆļČäņäØĻ│╝ ļ»╝Ļ░Éņä▒ ļČäņäØ
ļłäņĀü ļ®öĒāĆļČäņäØņØĆ ņŗ£Ļ░äņØś ĒØÉļ”äņŚÉ ļö░ļØ╝ ņŚ░ĻĄ¼ Ļ▓░Ļ│╝Ļ░Ć ņ¢┤ļ¢╗Ļ▓ī ļ│ĆĒĢśļŖöņ¦Ć ņČöņĀüĒĢśļŖö ļ░®ļ▓Ģņ£╝ļĪ£ ņŻ╝ļĪ£ ņŚ░ĻĄ¼ļōżņØä ņČ£ĒīÉ ņŚ░ļÅäļ│äļĪ£ ņĀĢļĀ¼ĒĢ┤ļ│┤ļ®┤ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņØś ļ│ĆĒÖö ņČöņØ┤ļź╝ ĒīīņĢģĒĢĀ ņłś ņ׳ļŗż[1,2]. ļśÉļŗżļźĖ ļ░®ļ▓Ģņ£╝ļĪ£ļŖö Ēæ£ļ│ĖņØ┤ Ēü░ ņŚ░ĻĄ¼ļČĆĒä░ ņ░©ļĪĆļĪ£ Ēł¼ņ×ģĒĢśņŚ¼ ĒÜ©Ļ│╝ Ēü¼ĻĖ░Ļ░Ć ņ¢┤ļ¢╗Ļ▓ī ļ│ĆĒĢśļŖöņ¦Ć Ļ┤Ćņ░░ĒĢśļŖö ļ░®ļ▓ĢļÅä ņ׳ļŗż. ņØ┤ļĢī Ēæ£ļ│Ė Ēü¼ĻĖ░Ļ░Ć ņ×æņØĆ ņŚ░ĻĄ¼ļōżņØ┤ Ēł¼ņ×ģļÉśņ¢┤ļÅä ĒÜ©Ļ│╝ Ēü¼ĻĖ░Ļ░Ć Ļ▒░ņØś ļ│ĆĒĢśņ¦Ć ņĢŖļŖöļŗżļ®┤ small-study efffectĻ░Ć Ļ▒░ņØś ņŚåļŖö Ļ▓āņ£╝ļĪ£ ĒĢ┤ņäØĒĢĀ ņłś ņ׳ļŗż. ļ»╝Ļ░Éņä▒ ļČäņäØņØ┤ļ×Ć ļČäņäØņØś ĻĖ░ņżĆņØ┤ļéś ļé┤ņÜ®ņŚÉ ļö░ļØ╝ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ ņ¢┤ļ¢╗Ļ▓ī ļ│ĆĒĢśļŖöņ¦Ć Ļ▓ĆĒåĀĒĢśļŖö ļ░®ļ▓Ģņ£╝ļĪ£ ļČäņäØļÉ£ Ļ▓░Ļ│╝Ļ░Ć ņ¢╝ļ¦łļéś ņØ╝Ļ┤Ćņä▒ņØ┤ ņ׳ļŖöņ¦Ć ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ ņŗ£Ē¢ēĒĢ£ļŗż[1].
Ļ▓░Ļ│╝ ļ│┤Ļ│Ā
ņØ╝ļ░śņĀüņ£╝ļĪ£ ļ®öĒāĆļČäņäØņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØĆ ļ│┤Ļ│Ā ĒśĢņŗØņØä ņĘ©ĒĢ£ļŗż[1].
1) ņä£ļĪĀ
2) ņŚ░ĻĄ¼ ļ░®ļ▓Ģ
ŌĆóĒżĒĢ©ļÉ£ ņŚ░ĻĄ¼ļŹ░ ļīĆĒĢ£ ĻĖ░ņżĆ
ŌĆóļ¼ĖĒŚī Ļ▓Ćņāē
ŌĆóņäĀņĀĢļÉ£ ņŚ░ĻĄ¼ņØś ņ¦ł Ļ▓Ćņ”Ø
ŌĆóļ│ĆņłśņØś ņĮöļö®
ŌĆóļŹ░ņØ┤Ēä░ ļČäņäØ ļ░®ļ▓Ģ
3) ļČäņäØ Ļ▓░Ļ│╝
ŌĆóļ®öĒāĆļČäņäØņŚÉ ĒżĒĢ©ļÉ£ Ļ░£ļ│ä ņŚ░ĻĄ¼ņØś ņ¦ł Ļ▓Ćņ”Ø
ŌĆóĒÜ©Ļ│╝ Ēü¼ĻĖ░ ļ░Å Forest plot
ŌĆóĒÅēĻĘĀ ĒÜ©Ļ│╝ Ēü¼ĻĖ░ņØś ņé░ņČ£ ļ¬©ĒśĢ
ŌĆóņĪ░ņĀł ĒÜ©Ļ│╝ ļČäņäØ
ļŹ░ņØ┤Ēä░ ņśżļźś Ļ▓Ćņ”Ø
4) ļģ╝ņØś ļ░Å Ļ▓░ļĪĀ
5) ņ░ĖĻ│Āļ¼ĖĒŚī
6) ļČĆļĪØ
ļ®öĒāĆļČäņäØņØä ņ£äĒĢ£ ĒöäļĪ£ĻĘĖļש
Ļ░Ćņן ļäÉļ”¼ ņé¼ņÜ®ļÉśļŖö ĒöäļĪ£ĻĘĖļשņ£╝ļĪ£ļŖö ļ»ĖĻĄŁņØś Biostatņé¼ņŚÉņä£ ļ¦īļōĀ Comprehensive Meta-AnalysisĻ░Ć ņ׳ļŗż. ĻĖ░ļŖźļÅä ļŗżņ¢æĒĢśĻ│Ā ļ¦żņÜ░ ņé¼ņÜ®ĒĢśĻĖ░ ņēĮĻ▓ī ļ¦īļōżņ¢┤ņĀĖ ņ׳Ļ│Ā ĻĘĖļלĒöĮļÅä ĒøīļźŁĒĢśļŗż. ņ×ÉņäĖĒĢ£ tutorialļÅä Ļ░ĢņĀÉņØ┤ļŗż. ļŗżļ¦ī ļ¦żĒĢ┤ ļ╣äņÜ®ņØä ņ¦ĆļČłĒĢśļŖö ļ░®ņŗØņØ┤ļØ╝ ņŚ░ĻĄ¼ņ×ÉņŚÉĻ▓ī ļŗżņåī ļČĆļŗ┤ņ£ä ļÉĀ ņłś ņ׳ļŗż. STATAļŖö ļ¬ģļĀ╣ļ¼ĖņØä ņé¼ņÜ®ĒĢ┤ņĢ╝ ĒĢśļŖö ņ¢┤ļĀżņøĆņØ┤ ņ׳ņ¦Ćļ¦ī, ļŗżļ│Ćļ¤ē ļ®öĒāĆļČäņäØņØ┤ļéś ļäżĒŖĖņøīĒü¼ ļ®öĒāĆļČäņäØ ļō▒ Ļ│ĀĻĖēĻĖ░ļŖźņØä ņĀ£Ļ│ĄĒĢ£ļŗż. ļ¼┤ļŻī ĒåĄĻ│ä ĒöäļĪ£ĻĘĖļשņØĖ RņØä ņØ┤ņÜ®ĒĢ┤ņä£ļÅä ļ®öĒāĆļČäņäØņØ┤ Ļ░ĆļŖźĒĢ£ļŹ░, ŌĆ£metaŌĆØņØ┤ļéś ŌĆ£metaforŌĆØ ĒÄśĒéżņ¦Ćļź╝ ņäżņ╣śĒĢśļ®┤ ļÉ£ļŗż. ļśÉĒĢ£ ĻĄŁļé┤ ņŚ░ĻĄ¼ņ¦äņŚÉ ņØśĒĢ┤ ņÜ┤ņśüļÉśļŖö ŌĆ£ņø╣ņŚÉņä£ ĒĢśļŖö R ĒåĄĻ│äŌĆØ ņé¼ņØ┤ĒŖĖņŚÉ Ļ░Ćņ×ģĒĢśļ®┤ RņŚÉņä£ ļ¬ģļĀ╣ļ¼ĖņØä ņ×ģļĀźĒĢĀ ĒĢäņÜö ņŚåņØ┤ graphical user inferface(GUI) ļ░®ņŗØņ£╝ļĪ£ ņēĮĻ▓ī ļ®öĒāĆļČäņäØņØä ņ¦äĒ¢ēĒĢĀ ņłś ņ׳ļŗż[1].
Ļ▓░ ļĪĀ
ļ®öĒāĆļČäņäØņØĆ ļŗżņ¢æĒĢ£ ņØśĒĢÖņĀü ņ¦łļ¼ĖņŚÉ Ēśäņ×¼Ļ╣īņ¦Ć Ļ░Ćņן ņ”ØĻ▒░ļĀź ļåÆņØĆ ļŗĄļ│ĆņØä ņĀ£Ļ│ĄĒĢśļŖö ļ░®ļ▓ĢņØ┤ļŗż. ĒĢśņ¦Ćļ¦ī ņĀĢĒÖĢĒĢ£ ļ®öĒāĆļČäņäØņØä ņłśĒ¢ēĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ļ®öĒāĆļČäņäØņØś ĻĘ╝Ļ░äņØä ņØ┤ļŻ©ļŖö Ļ░ĆņĀĢļōżĻ│╝ ļ®öĒāĆļČäņäØņØś ĒĢ£Ļ│ä ļ░Å ņśżļźś Ļ░ĆļŖźņä▒ņŚÉ ļīĆĒĢ┤ņä£ ņČ®ļČäĒ׳ ņłÖņ¦ĆĒĢśļŖö Ļ▓āņØ┤ ĒĢäņłśņĀüņØ┤ļŗż.




 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print